В качестве примера рассмотрим задачу: «Два мотоциклиста выехали одновременно из пунктов А и В навстречу друг другу и встретились в 50 км от В. Прибыв в пункты А и В, мотоциклисты сразу же повернули назад и встретились вновь в 25 км от А. Сколько километров между А и В?»

Решение этой задачи с помощью уравнения представляет для учащихся определенные трудности: не случайно в школьном учебнике аналогичная задача помещена в разделе «Задачи повышенной трудности для 8 класса».

На наших занятиях учащиеся решали эту задачу, не составляя уравнения, а рассуждая так. От начала движения до первой встречи оба мотоциклиста проехали расстояние равное АВ, а к моменту второй встречи проехали втрое большее расстояние. Таким образом, каждый из них до второй встречи проехал втрое больше, чем до первой. Мотоциклист, выехавший из пункта В, до первой встречи проехал 50 км. Следовательно, до второй встречи он проехал 150 км (50 ´ 3 = 150). Поэтому расстояние от А до В равно 125 км (150 – 25 = 125).

При таком подходе эту задачу могут решить учащиеся не только VIII, но и V класса.

Арифметический способ решения задач, когда шаблонный метод не легко приводит к результату, является, как свидетельствуют наши наблюдения, одним из лучших средств развития самостоятельного, творческого решения учащихся. С помощью специально подобранных задач, которые могут заинтересовать учащихся своей кажущейся простотой и тем, что их решение не сразу дается в руки, можно показать учащимся красоту, простоту и изящество логического рассуждения, приводящего к решению задачи. Иллюстрацией сказанного служит задача № 1287 из [5]. (Всадник и пешеход одновременно отправились из пункта А в пункт В. Всадник, прибыв в пункт В на 50 мин. раньше пешехода, возвратился обратно в А. На обратном пути он встретился с пешеходом в двух километрах от В. На весь путь всадник затратил 1 час 40 минут. Найдите расстояние от А до В и скорость всадника и пешехода.)

Рассматривая решение задач несколькими способами, учитель на уроке и во внеклассной работе должен ориентировать учащихся на поиски красивых, изящных решений. Тем самым учитель будет способствовать эстетическому воспитанию учащихся и повышению их математической культуры.

Решая с учащимися ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая — помочь ученику решить именно данную задачу, научить его решать задачи, аналогичные рассматриваемой; вторая — так развить способности ученика, чтобы он мог в будущем решить любую задачу школьного курса самостоятельно. Эти две цели, безусловно, связаны между собой, так как, справившись с заданной достаточно трудной для него задачей, учащийся несколько развивает свои способности к решению задач вообще.

Поэтому, преследуя вторую цель, при решении задач несколькими способами мы обращали внимание учащихся не только на наиболее рациональный, красивый способ решения данной задачи, но и на те способы, которые широко применяются при решении других задач и в некоторых случаях оказываются единственными. Поясним сказанное примером.

При решении задачи «Что больше: или 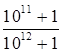?» ([5], № 1263) учащиеся, как правило, применяют наиболее естественный в данном случае способ решения — приведение дробей к общему знаменателю и сравнение их числителей.