Пусть даны две переменные х и у. Говорят, что переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого, значения х однозначно определить значение у.

Примеры функций:

1. y = kx+b.

2. у= |х|.

3. у = х2.

4. у= 1/х, х>0

5. у = √х.

В каждом из этих примеров указана формула, позволяющая для каждого значения переменной х однозначно вычислить значение переменной у.

Для того чтобы задать функцию, нужно:

указать множество всех возможных значений переменной х. Это множество, которое мы будем обозначать D, называют областью определения функции;

указать правило, по которому каждому числу х из множества D сопоставляется число у, определяемое числом х. Это число у называется значением функции в точке х. Переменную х называют аргументом.

Функция обычно обозначается одной буквой, например f. Значение функции f в точке х обозначается f (х).

Итак, если задана функция f, то задано множество чисел D и каждому числу xD сопоставлено число y = f(x).

Пусть задана функция f. с областью определения D. Рассмотрим координатную плоскость. По оси абсцисс будем откладывать значение аргумента, а по оси ординат — значение функции. Для каждого числа xD можно вычислить y = f(x) и построить точку М (х; f (х)). Множество всех таких точек образует кривую, называемую графиком функции / в заданной системе координат.

Итак, графиком функции f называется множество точек плоскости с координатами (х; f(х)), где х пробегает область определения функции f.

На рисунке 2 изображены графики функций, которые были приведены в качестве примера в начале параграфа.

Рассмотренные нами ранее простейшие зависимости определяют три важнейшие функции:

Эти функции являются стандартными примерами функций из трех классов, с которыми мы будем часто сталкиваться в дальнейшем: линейных, дробно-линейных и квадратичных.

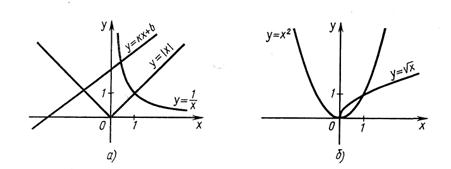
Рис. 2

Для того чтобы определить переменную у как функцию от переменной х, нужно задать множество значений аргумента х и указать правило вычисления значений у в зависимости от х. Сначала обсудим, как задается правило вычисления значений. Во всех приведенных ранее примерах правило вычисления задавалось формулой, содержащей определенные операции.

Обучаясь математике, мы знакомились с различными действиями, операциями над числами. Например, используя только сложение и умножение, мы можем из числа х получить новые числа, скажем 3х, 3х + 5, х3 + 3х + 5 и т. д. Уже такого рода выражения, многочлены, могут служить для построения довольно богатого запаса функций.

Использование деления сильно расширяет этот запас, позволяет образовать выражения вида и т. п. Функции, которые строятся как отношения многочленов, называют рациональными.

Операция деления отличается от сложения и умножения тем, что она не всегда определена — в знаменателе дроби нельзя ставить нуль. Поэтому, например, в выражение можно подставить любые числа, кроме х=1 и х=-1, при которых знаменатель равен нулю.

Появление новых операций и введение специальных знаков для их обозначения приводят к дальнейшему обогащению наших возможностей — извлечение корня, переход к модулю числа и т. п.

Например, пусть f (х) равно числу —1, если х<0, равно нулю, если х = 0, и равно 1, если х>0. Этими словами мы описали некоторое правило вычисления, применимое к любому числу. Обозначим число f (х), найденное по этому правилу, через sgn х (от латинского слова signum, что означает «знак»). Теперь мы с помощью символа для обозначения новой операции можем строить новые формулы, например