Теоретический материал электронного учебника
2. (-1 - i) - (2 + 3i) = -3 - 4i.
3. (10 - i)(2 + i) = 21+8i.
4. 
.
Геометрически комплексные числа можно изображать точками плоскости, абсциссами которых служат действительные части, а ординатами - коэффициенты при мнимой единице. Таким образом, если z= a+bi, то на плоскости ХОУ это будет точка М(а, b). Так как любой вектор плоскости с началом в точке O(0,0) определяется координатами конца, то комплексные числа также изображают радиус – векторами (рис. 1).
Рис. 1
Кроме алгебраической формы комплексное число может быть записано с помощью тригонометрической формы. Введем следующие определения.
О п р е д е л е н и е. Модулем комплексного числа z= а+ bi называется арифметический квадратный корень из суммы квадратов его действительной части и коэффициента при мнимой единице: |z| = r = 
.
О п р е д е л е н и е. Аргументом комплексного числа z = а + bi называется число 
, для которого 
.
Возьмем на плоскости точку М(а, b), пусть ей соответствует комплексное число z = а + bi. Обозначим через j угол, который образует радиус – вектор ОМ с положительным направлением оси ОХ.
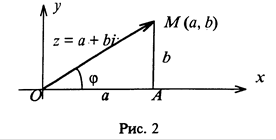
Из D ОМА (рис.2) AO = OMcosj, AM = ОМsinj, но ОМ= = г, ОА =а; AM =b; тогда z = а + bi = rcosj + irsinj = r(cosj + isinj).
Запись числа z = r(cosj + isinj) называется тригонометрической формой комплексного числа.
С геометрической точки зрения, модуль комплексного числа представляет собой длину радиус-вектора, который это число изображает, а аргумент - это угол, который образует данный радиус-вектор с положительным направлением оси ОХ.
П р и м е р. Найти модуль, аргумент и записать число z = 1- i в тригонометрической форме.
Имеем r =
= 
; cosj =
; sinj =
; тогда j =
и 
.
Используя тригонометрическую форму комплексного числа, умножение и деление комплексных чисел можно выполнять так: если 
, 
, то z1z2 = r1r2[cos (j1+j2) + isin (j1+j2)],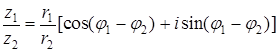 
.
Операции же возведения в целую степень и извлечения корня удобнее проводить в тригонометрической форме. Так, для возведения в целую степень n комплексного числа z = r(cosj + isinj) известна формула Муавра:
zn = rn(cos nj + isin nj).
|
|
Отметим, что возведение комплексных чисел в натуральную степень можно выполнять и в алгебраической форме, просто перемножая число само на себя или воспользовавшись биномом Ньютона. |
П р и м е р. Найти (2 + 2i)5.
Если z = 2 +2i, то r =
, cosj = , sinj = , j = 
. Тогда
, а 
.
Для извлечения корня степени n Î N
из комплексного числа z = =r(cos j + isin j ) используется следующая формула:
, k = 0, 1, 2, ., n-1.
П р и м e p. Найти 
. Найдем тригонометрическую форму подкоренного выражения:
; 
; 
; 
; 
.