Описание опытно-экспериментальной работы
1. Образовательная:
познакомить и научить учащихся построению некоторых правильных многоугольников с помощью циркуля и линейки.
2. Развивающая:
формировать научное мировоззрение и пространственное воображение учащихся.
3. Воспитательная:
выработать внимание и самостоятельность при работе на уроке.
Ход урока:
1. Организационный момент.
2. Актуализация.
3. Объяснение нового материала.
4. Первичное закрепление изучаемого материала.
5. Подведение итогов урока.
6. Предъявление домашнего задания.
| Деятельность учителя | Деятельность ученика | ||||||||||
|
1. Организационный момент. Здравствуйте. Сегодня у нас необычный урок – бинарный, то есть вас будут учить одновременно два учителя: геометрии и черчения. Таким образом, мы попробуем проследить аналогию между этими предметами. Откройте тетради. Запишите число, тему. |
Открывает тетради, записывают. | ||||||||||
|
2. Актуализация. Для начала повторим. Учитель геометрии. Какой многоугольник называется правильным? Запишите на доске все формулы, изученные на прошлом уроке. Учитель черчения. Какие геометрические построения вам известны? |
Правильным многоугольником называется многоугольник, у которого все стороны и все углы равны. | ||||||||||
|
3. Изучение новой темы. Учитель геометрии. Тема нашего урока: «Построение правильных многоугольников». Учитель черчения. Название темы, которую предлагаю вам я: «Деление окружности на равные чести».
Построением правильных фигур мы уже занимались, когда строили правильный четырехугольник (квадрат) и правильный треугольник (равносторонний). Вспомните и покажите нам как это делать. Учитель черчения. А вы знаете, в черчении тоже есть задачи, где нужно построить квадрат и правильный треугольник, только строится это по-другому и цель данного построения – разделить окружность на три равные части. Для этого надо поставить опорную ножку циркуля в конец диаметра, описать дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра. Мы разделили окружность на три равные части. Теперь, если мысленно соединить полученные точки, то увидим правильный треугольник. Для того, чтобы разделить окружность на четыре равные части, всего-навсего надо
   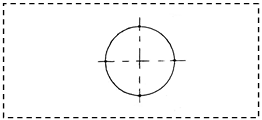 провести два взаимно перпендикулярных диаметра. провести два взаимно перпендикулярных диаметра.
Перпендикулярные прямые вы строить умеете. Полученные точки и являются делящими окружность на четыре равные части. И опять, если мы мысленно соединим полученные точки, получим квадрат. Учитель геометрии. Ну а теперь, перейдем к построению более сложных многоугольников. Задача 1. Построить правильный шестиугольник, сторона которого равна данному отрезку. Для решения этой задачи, воспользуемся формулой 6. Запишите ее. Что это значит? Правильно. Значит нам надо построить окружность у которой радиус равен стороне. Затем отметим на ней произвольную точку (А1). После этого, не меняя раствор циркуля, построим на окружности точки (А2), (А3), (А4), (А5), (А6) так, чтобы выполнились равенства А1А2=А2А3=А3А4=А4А5=А5А6.
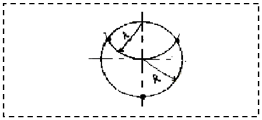
Учитель черчения. Что надо сделать с окружностью для того, чтобы построить правильный шестиугольник? Вот именно. Этим мы сейчас и займемся, и первое что мы сделаем, это раствор циркуля установим равным радиусу R окружности. Почему? Правильно. То есть, смотрите, мы делаем все так, как и в геометрии. Дальше немного по другому. Из противоположных концов одного из диаметров окружности описываем дуги. Полученные точки делят окружность на равные части. Вот таким образом. Учитель геометрии. Итак, мы с вами уже знаем два способа построения шестиугольника: способ построения в геометрии и способ построения в черчении. Они очень похожи. Но кроме этих существует еще один способ. Дан правильный n-угольник. Построить правильный 2n-угольник. Для этого достаточно около правильного n-угольника описать окружность. Для этого построим биссектрисы углов и обозначим точку их пересечения буквой О, это будет центр окружности, описанной около квадрата. Для решения задачи достаточно разделить дуги А1А2, А2А3, А3А4, А4А1 пополам, проведя серединные перпендикуляры к сторонам данного многоугольника. И каждую из точек деления соединить отрезками с концами соответствующей дуги. Таким образом, построен правильный восьмиугольник. И таким образом можно построить все 2n-угольники. Учитель черчения. И в завершении объяснения новой темы разберем построение восьмиугольника в черчении, то есть, как разделить окружность на 8 равных частей. Чтобы разделить окружность на 8 равных частей, достаточно провести две пары диаметров, одна пара проведена по линейке и катету равнобедренного угольника, другая пара по линейке и гипотенузе угольника. Таким же образом можно строить правильный восьмиугольник в геометрии. Учитель геометрии. На этом мы заканчиваем объяснение нового материала и приступим к закреплению. |
Деление отрезка на равные части; построение углов, перпендикулярные и параллельные прямые, треугольника по трем элементам и другое. | ||||||||||
| 4. Первичное закрепление изучаемого материала. | |||||||||||
|
1. 2. Данную окружность впишите в квадрат. 3. Разделите окружность на 6 равных частей. 4. Постройте правильный восьмиугольник, используя метод построения из геометрии. 5. С помощью циркуля и линейки в данную окружность впишите правильный шестиугольник, сторона которого равна данному отрезку. | |||||||||||
| 5. Подведение итогов урока. | |||||||||||
|
И так, сегодня мы провели с вами бинарный урок с участием учителя геометрии и черчения. Что вы почерпнули из этого урока? Он вас чему-нибудь научил? Ну и отсюда можно сделать вывод, что геометрия и черчение, хоть и не одинаковые предметы, многое в них разное, но они взаимно дополняют друг друга и, тем самым, расширяют ваши возможности для дальнейшего развития. |
На этом уроке мы научились строить многоугольники, а благодаря учителю черчения эти задачи мы можем выполнять двумя способами. | ||||||||||
| 6. Предъявление домашнего задания. | |||||||||||
|
Постройте с помощью циркуля и линейки правильный шестиугольник, две вершины которого лежат на горизонтальной центровой линии. | |||||||||||
10-


 Учитель геометрии.
Учитель геометрии.


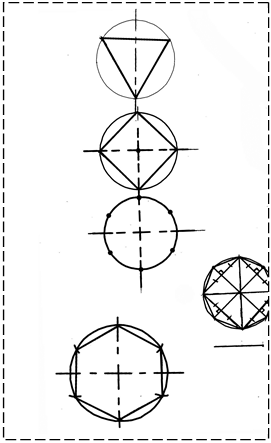
 Постройте правильный треугольник используя метод построения из геометрии.
Постройте правильный треугольник используя метод построения из геометрии.